Projective Geometry Lesson 10

Projective Floor and Ceiling Come Together

I’ve started to really introduce some mind-contorting concepts to you, and I hope you’re enjoying the process.  It’s not my intention to prove anything to you, but rest assured that everything in Projective Geometry is provable in a strictly mathematical sense, if that’s your desire (you can look it up!).  Rather, I will keep presenting you with pictures to imagine, especially pictures that you put into motion in your mind; and, through those pictures, you can come to grow some new mental muscles and new ability to visualize.

If you’ve come this far, you might already be asking yourself, “This is all very well and good, but what is the benefit of building these new muscles, or the use of imagining things like points or lines at infinity?”  I think this is a valid question, and I’d like to bring you, soon, some of the ”fruits”  that can help you appreciate why PG is important as a mental exercise that can prepare someone to think holistically.  As a little preview, I’ll say that today we have a strong and largely unconscious “point-centered” bias in our ways of working, and in our science and our technology. Witness our obsession with subatomic particles in our quantum physics, but our simultaneous puzzlement about a massive amount of “dark matter” in the universe that seems necessary to make the equations work out but which nobody yet understands.  We are mostly unaware of the much larger context in which everything in nature (including human beings) operates.  PG is one good way to attain more of this holistic point of view.  It is not the only way. For instance, I see similar influences in the work of Robin Wall Kimmerer in her book Braiding Sweetgrass: Indigenous Wisdom, Scientific Knowledge and the Teachings of Plants.  Another pathway toward holistic “Goethean science” that I’d recommend is the three-part podcast series found on this link about Where Does an Animal End?: The American Bison from the Nature Institute.  All of these paths lead us to pay attention to the surroundings (sometimes also called the “periphery) in new ways that are good for us, and good for our relationship with the living Earth.

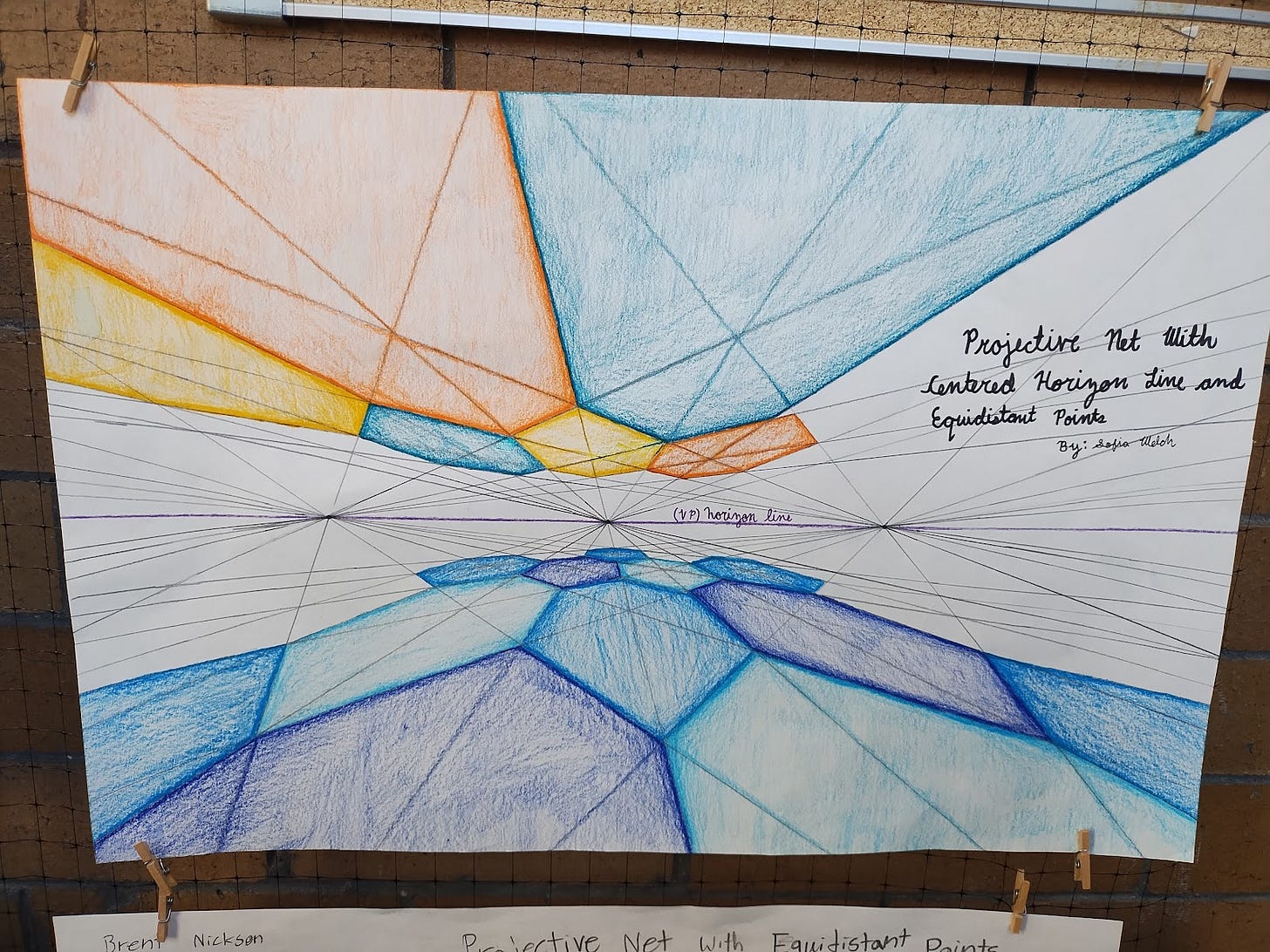
So . . . if you want to continue down the PG path, try this one.  Imagine that you created a Net drawing, but instead of placing the horizon at the top of the page, you placed it in the middle, and then you did the usual Net construction, but built a Net both above and below the line.  This is a great drawing challenge if you enjoyed the Net drawing process, and it arises pretty naturally if you just apply the same skills, but it’s a little difficult to describe how to do it in words. Basically you build one Net, for example down below, and as you fill in the lines, you find that by simply extending your lines all the way across the page you are building another Net up above.   Here is an extra credit drawing done by a student in my class:

Pretty awesome, right? What you get is two infinite planes, one above and one below, both receding to the infinite horizon in the distance.

Can you imagine that arrangement: basically an infinite floor and an infinite ceiling, with no walls in any direction. . .?  Try to imagine that now. In your imagination, as you stand on the “floor” and under the “ceiling,” and turn your gaze around, you see the infinite horizon, in every direction.  Now, imagine that the ceiling begins to tilt in one particular direction, perhaps tilting gently down in front of your gaze.  As it tilts more and more, what do you see in your mind?  Can you see the line where the two planes meet each other coming toward you?  Two infinite planes meeting each other in space form one line.  This is like a 3-D version of the 2-D Kepler’s Propellor exercise.  Just as the Kepler’s propellor line causes the sliding point to come closer and then shoot off “to infinity”, in the same manner as the “ceiling plane” tilts, the line where they meet also slides in, coming close to your imaginary viewing position.  In your mind, you can make the ceiling tilt and in any direction that it tilts, that is the direction that the meeting line of floor and ceiling goes.  Logically, then, when the floor and ceiling are not tilted relative to each other (in other words, when they are parallel), their meeting line is at infinity . . . and it can be reached in every direction equally along the plane!

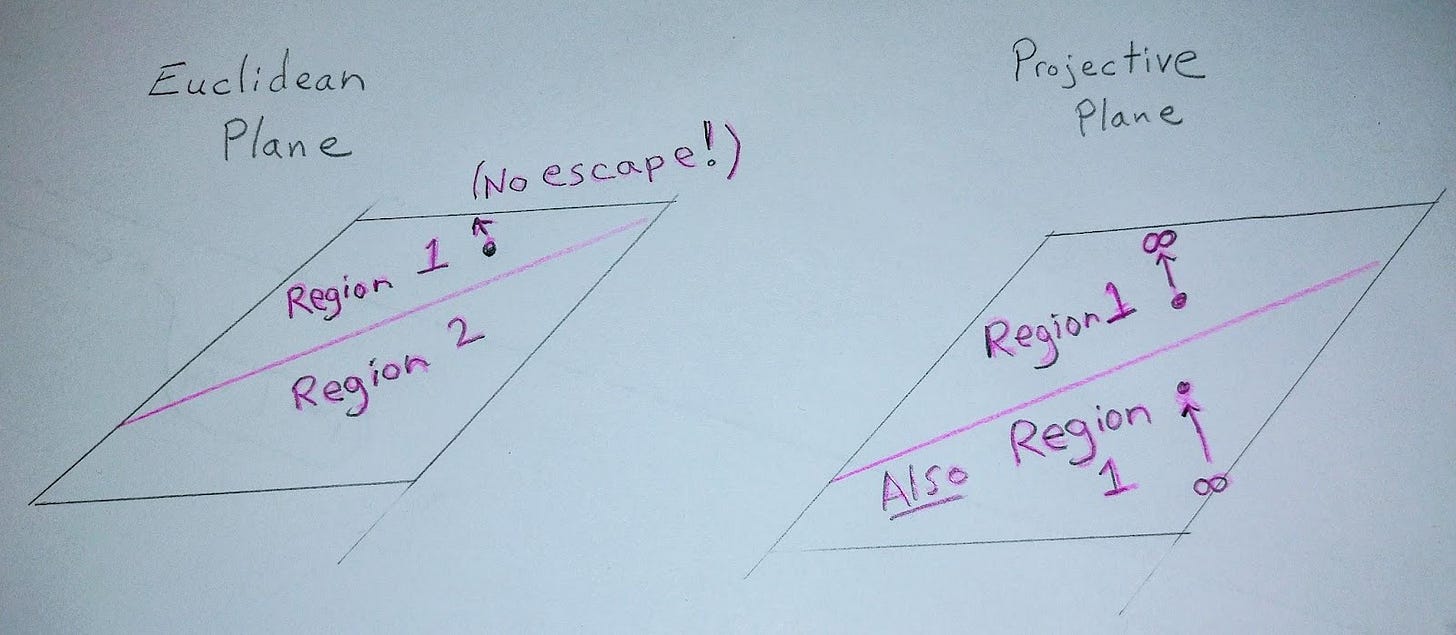
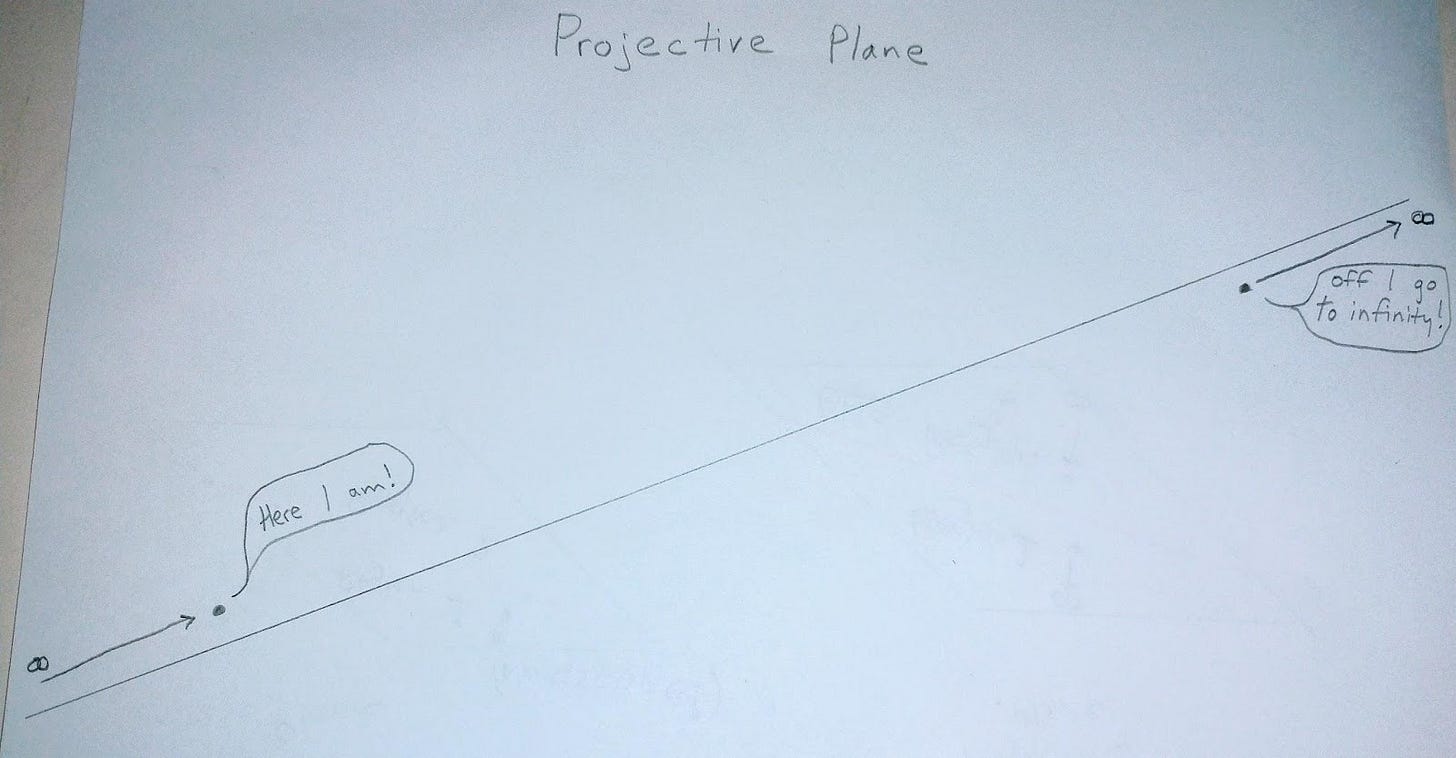
Let’s push this imagination a little further.  Now imagine just one infinite plane, and then in your imagination draw one line that lies in that plane.  If this is a Projective plane, then we know that we have a way to “shoot off to infinity” and return “from the other side”.  So, whereas in Euclidean geometry, drawing a line (even a line of indefinite length) in the plane separates the plane into two distinct regions, doing the same in a Projective plane does not.  A free point on one side of a Projective line could “slide” out to infinity (exactly as we pictured it in the Kepler's Propellor exercise) and would appear “on the other side” of the line.  

Interestingly, and quite hard (or even impossible) to imagine in a visual way, even if the point slides along hugging the line all the way, when it returns, it will have found its way to the “other side.”  

This is possibly the hardest paradox to wrestle with yet.  How is it that a point, traveling out to infinity along a line, can pass through infinity and end up back again, but on what we think of as “the other side” of the line?  A Projective line seems to be very like a Mobius strip, in that it is continuous, infinite, and cycles back upon itself in a twisty sort of way. . .

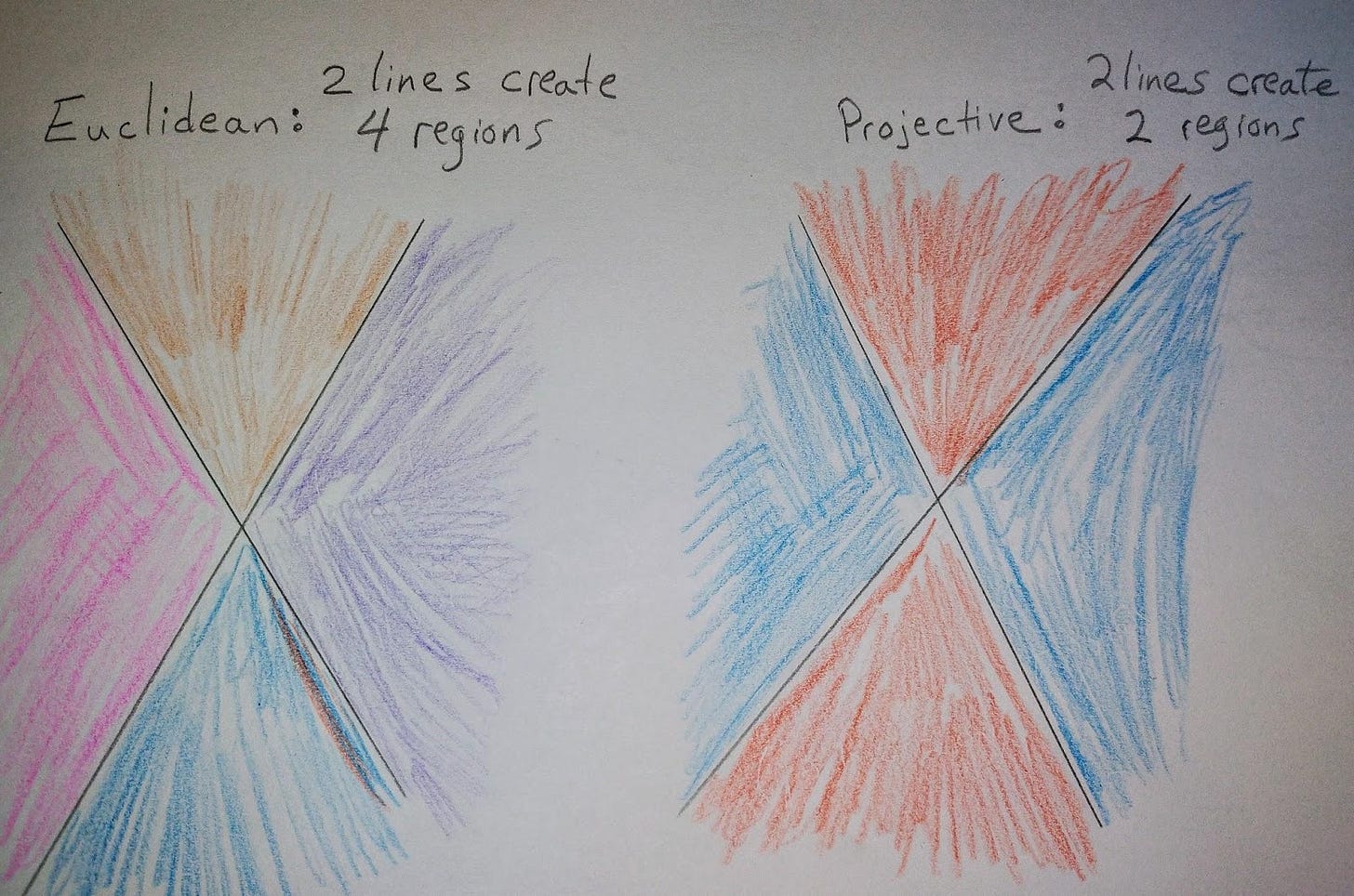
Now let’s add another line to this imagination.  If I drew two crossed lines in a plane, and if I were thinking in a Euclidean way, I’d say that I had made four distinct regions. . . whereas in Projective Geometry, I would have made only two. Here I will start to use colors to show the different regions.  If you want to draw and color along with me, this is another one of those simple but profound drawing exercises that gets you into thinking about it more deeply through doing it.  You are not only coloring on a piece of paper . . .your imagination is coloring infinite swaths!

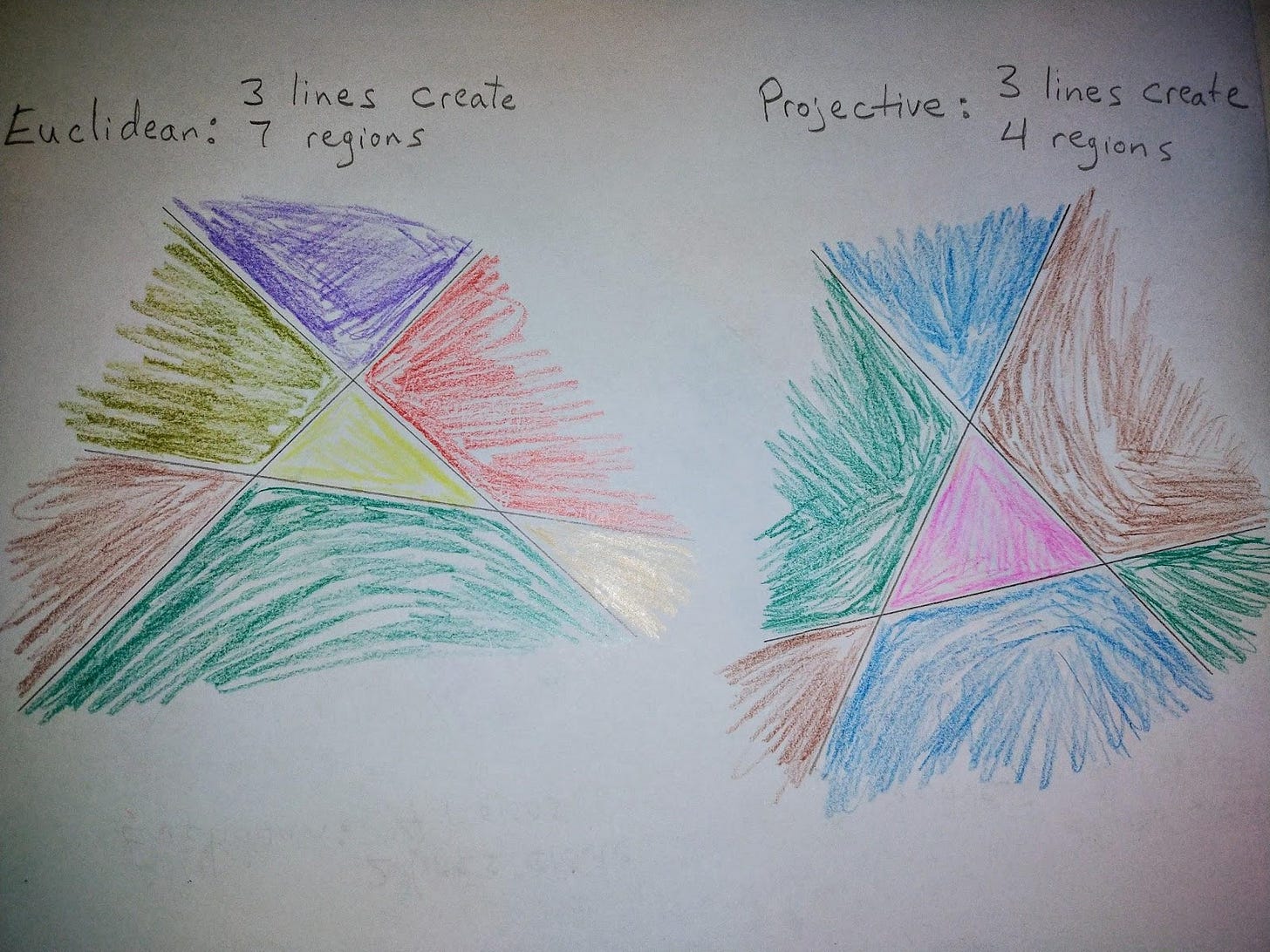
Can you understand, and even feel, how the Projective plane is continuous with itself “through infinity”?  Typically this brings up a fair amount of puzzlement and wonder, and even some rejection.  Be honest with yourself about how you react to this!  Write your questions and challenges in the comments!  Be open to the idea that these new realities of Projective geometry are truths that are essentially un-picturable (and yet are mathematically just as logical as Euclidean geometry).  Let’s now draw three lines, not all passing through the same point, and compare Euclidean to Projective ways of thinking about it.  How many regions now in each case? See if you can do it before you look at my picture!

.

.

.

.

.

.

Is this what you thought?  Three lines in the Euclidean plane creates 7 regions, whereas in the Projective plane it creates 4.  3 of the 4 regions “pass through infinity” and one of them does not. . . and yet, (try to wrap your mind around this), all four regions are triangles!  Each region is bounded by exactly three lines.

We’ve done plenty for one post!  The PG posts will start coming at a much slower pace now, as I’m moving on to teaching Physics to 8th graders in a week.  I feel good about the foundation we’ve laid.  As I have time and opportunity, I’ll continue with more. . .