Projective Geometry Lesson 5

Only One Net!

Here are some of the excellent drawings done by some excellent 11th graders so far!

Here are Nets with equidistant points (colored in hexagonally):

Impressive, right?

And here are more Nets with unequal point distances (and colored in “quadrilaterally” rather than “hexagonally”):

We discovered in my last post that when you place three points on a line and start constructing your Projective Net, there is a fourth point that naturally appears, a convergence of all of the “missing diagonals” of the quadrilaterals that you are forming. You can see that in the picture of the quadrilateral Nets just above if you zoom in.  The students have found and labeled that fourth point.  (When we did the construction with equidistant points, this Harmonic Point appears to be missing because all of the diagonals are parallel to the horizon.  We’ll come back to that intriguing fact soon.)  Let’s explore this “Harmonic Point” a little further.

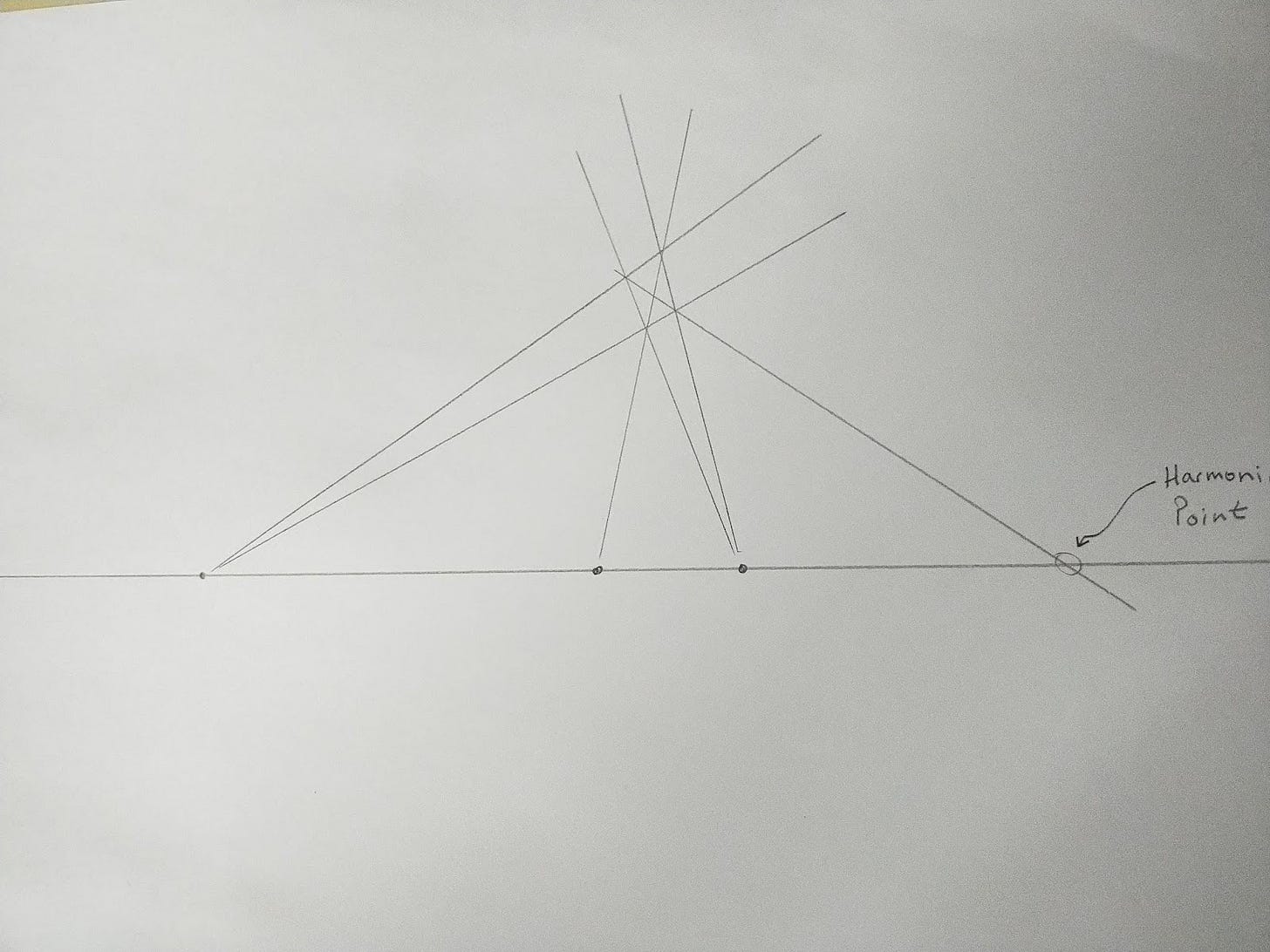
Draw your horizon line across the middle of your paper, leaving equal room above and below.  Now, choose your three points at unequal distances as before, and build the beginnings of a Net above your line, but leave the area below the line blank.  This is exactly the same construction that we did last time, we are just doing it above the horizon line.

Find the Harmonic Point by drawing in the missing diagonal:

Now: Do the very same construction below the line, but intentionally choose different angles for your lines to make a different-looking quadrilateral.  (Whoops, looks like I dropped a hair onto the paper too!:)

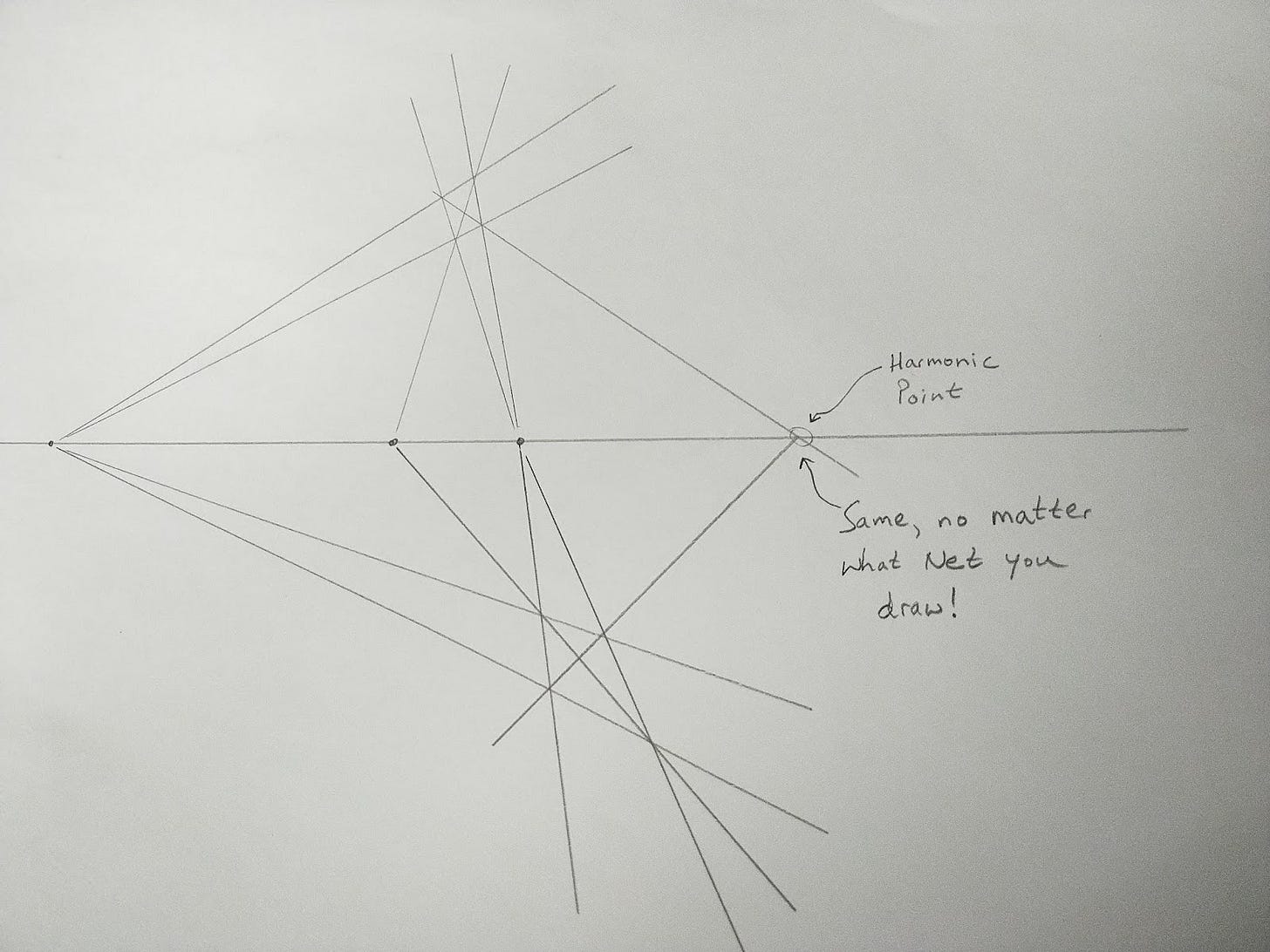
And, again, find the missing diagonal.  You will find quite amazingly that this diagonal connects directly to the same Harmonic Point.  

In fact, no matter how you construct the quadrilaterals, the Harmonic Point is always in the exact same place.  This leads to some immediate logical but perhaps surprising conclusions:

1. Since it doesn’t matter how you draw your Net, we should realize that all of the Nets are the exact same; they only look different because your choice of angle for your lines casts them into a different perspective.  There are not many different Nets, there is one Net, looked at from many different angles.

2. Because this is true, the placement of the Harmonic Point does not depend on the Net at all, even though constructing the Net allows you to find it.  Simply placing the three points on the line automatically places the fourth point for you.  You only have to do the construction to show that it is there.  Placing three points on a line automatically brings about a fourth point that somehow completes it.  

When we did these constructions in class last week, and we realized the above two facts, there were a lot of spontaneous “Whoa’s” from the students.  Whoa, indeed!  In the next installment, we will play with the Harmonic Point a little more, as it has much more to teach us.